4 Chapter 14: G-Estimation of Structural Nested Models
This is the code for Chapter 14.
library(tidyverse)
library(broom)
library(geepack)
library(boot)
library(cidata)4.1 Program 14.1
In this section, Hernán and Robins discuss rank preservation: that participants would be ranked in the same order for all counterfactual outcomes. We can’t do that, but we can look at the observed ranks. There are many ways to make ranks, but we’ll use dplyr::min_rank() and rank the participants in descending order of weights.
ranks <- nhefs %>%
mutate(
rank = min_rank(desc(wt82_71)),
lbl = if_else(
rank <= 3 | rank >= (max(rank, na.rm = TRUE) - 2),
round(wt82_71, 1),
NA_real_
)
) %>%
select(seqn, rank, lbl, wt82_71)
ranks %>%
select(-lbl) %>%
top_n(5, wt82_71) %>%
knitr::kable()| seqn | rank | wt82_71 |
|---|---|---|
| 1769 | 3 | 37.65051 |
| 5415 | 5 | 34.01780 |
| 6928 | 2 | 47.51130 |
| 22342 | 4 | 36.96925 |
| 23522 | 1 | 48.53839 |
ranks %>%
select(-lbl) %>%
top_n(-5, wt82_71) %>%
knitr::kable()| seqn | rank | wt82_71 |
|---|---|---|
| 5412 | 1563 | -29.02579 |
| 13593 | 1565 | -30.50192 |
| 21897 | 1562 | -25.97056 |
| 23321 | 1566 | -41.28047 |
| 24363 | 1564 | -30.05007 |
It’s easier to understand how the ranks are distributed in a plot. The heart of this plot is simply plotting the ranks (on the y axis) versus the observed change in weights. We’ll also label the top and bottom 3 ranks with geom_text_repel() from the ggrepel package. The people with the most weight loss are on the left while people with the most weight gain are on the right.
ranks %>%
ggplot(aes(y = rank, x = wt82_71)) +
geom_vline(xintercept = 0, col = "grey90", size = 1.3) +
geom_point(col = "#0072B2", size = 1, alpha = .9) +
ggrepel::geom_text_repel(
aes(label = lbl),
size = 4,
point.padding = 0.1,
box.padding = .6,
force = 1.,
min.segment.length = 0,
seed = 777
) +
theme_minimal(14) +
expand_limits(y = c(-200, 1700)) +
xlab("change in weight")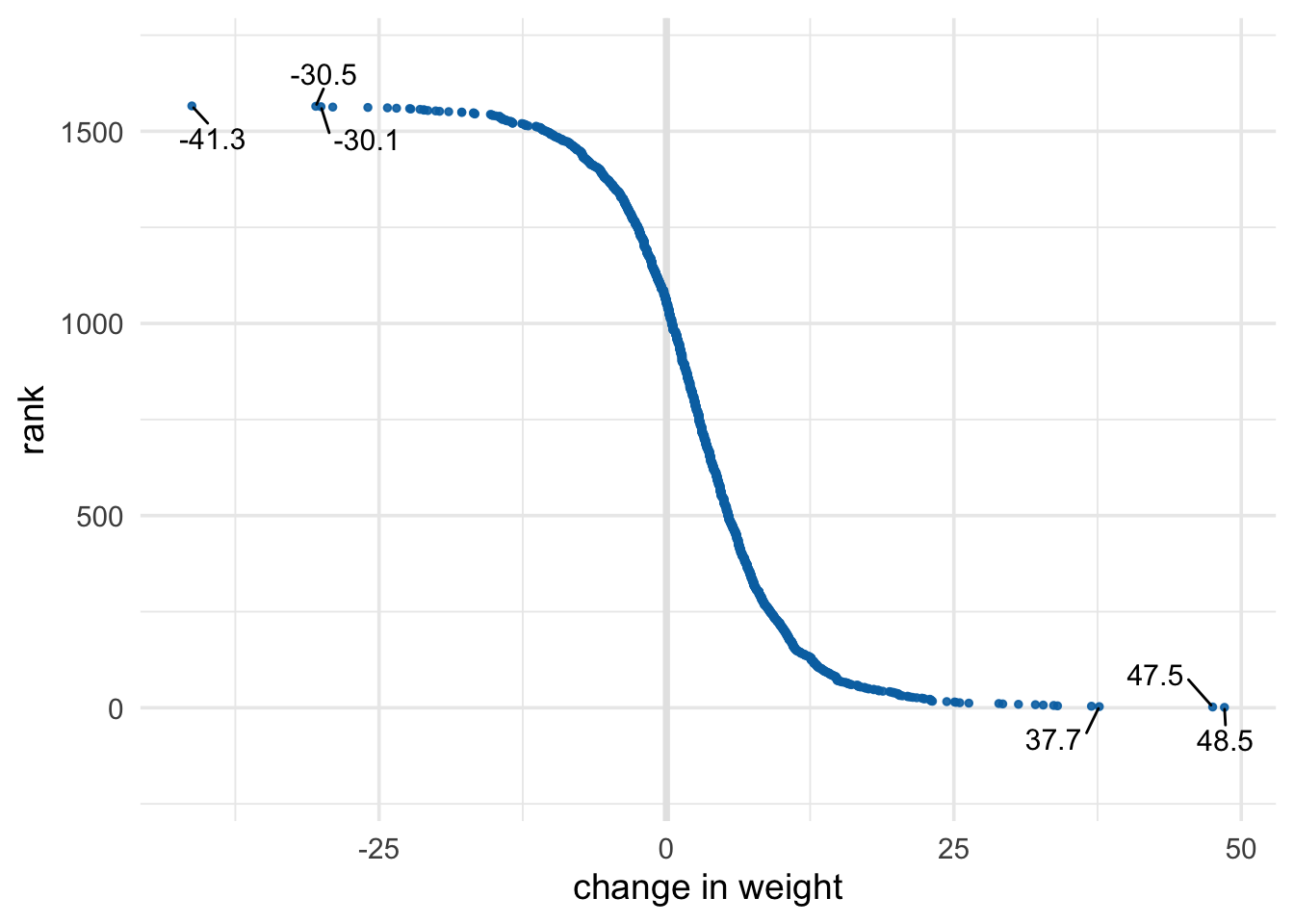
4.2 Program 14.2
We’ll start by quickly making censoring weights for the complete data set, nhefs_complete, as in Chapter 12.
# compute unstabilized inverse probability of censoring weights
cwts_model <- glm(
censored ~ qsmk + sex + race + age + I(age^2) + education +
smokeintensity + I(smokeintensity^2) +
smokeyrs + I(smokeyrs^2) + exercise + active +
wt71 + I(wt71^2),
data = nhefs_complete, family = binomial()
)
nhefs_complete <- cwts_model %>%
augment(type.predict = "response", data = nhefs_complete) %>%
mutate(cwts = 1 / ifelse(censored == 0, 1 - .fitted, .fitted))G-Estimation looks quite different than other types of causal regression models. Our main effect is not for wt82_71 but h_psi. Our goal is to find the regression model that minimizes h_psi so that it is independent of the outcome; we want it as close to the null as possible. h_psi is defined as the outcome minus the product of psi and the exposure. Then, we include h_psi in a model with the exposure as the outcome (qsmk) weighted by our censoring weights and adjusted for the confounders we’ve used in previous models. We’ll write a function, compute_h_psi(), to compute h_psi for a given value of psi.
In the book, Hernán and Robins tell us the best fit is 3.446, so we’ll test that the G-estimation model gives us a number very close to 0. The interpretation for this estimate is similar to the other causal modeling approaches: if everyone had quit smoking, they would have gained 3.446 more than if everyone had kept smoking.
# compute all values of h(psi)
compute_h_psi <- function(psi) {
df <- nhefs_complete %>%
mutate(h_psi = wt82_71 - psi * qsmk) %>%
# gee doesn't like missing values
drop_na(h_psi)
geeglm(
qsmk ~ h_psi + sex + race + age + I(age^2) + education +
smokeintensity + I(smokeintensity^2) +
smokeyrs + I(smokeyrs^2) + exercise + active +
wt71 + I(wt71^2),
data = df,
family = binomial(),
std.err = "san.se",
weights = cwts,
id = id,
corstr = "independence"
) %>%
tidy() %>%
filter(term == "h_psi") %>%
mutate(psi = psi) %>%
select(psi, estimate, p.value)
}
compute_h_psi(3.446)## # A tibble: 1 x 3
## psi estimate p.value
## <dbl> <dbl> <dbl>
## 1 3.45 0.000286 0.974The way that we have to find the best value for psi is by brute force: we will search values of psi within a plausible range. Here, we’ll check from 2 to 5 by values of .1, meaning we will actually fit 31 models. Then, we’ll figure out which value of psi produces the h_psi closest to null. To fit the models, we’ll map the compute_h_psi() function to each value with purrr::map_dfr(). (The map_dfr() returns a data frame, so we can manipulate it with dplyr.)
# search for h_psi for values of psi from 2 to 5 by .1
psi_search <- map_dfr(seq(2, 5, by = .1), compute_h_psi)Because we didn’t search quite as finely as the authors, we get an answer that is close but not quite what they have. Had we searched more finely (e.g. by = .001), we would have done so but would need to fit thousands of models.
Since we want the estimate closest to 0, we’ll sort by the absolute value of estimate.
psi_search %>%
arrange(abs(estimate))## # A tibble: 31 x 3
## psi estimate p.value
## <dbl> <dbl> <dbl>
## 1 3.5 -0.000735 0.934
## 2 3.4 0.00116 0.896
## 3 3.6 -0.00263 0.768
## 4 3.3 0.00304 0.729
## 5 3.7 -0.00453 0.612
## 6 3.2 0.00492 0.574
## 7 3.8 -0.00644 0.474
## 8 3.1 0.00679 0.435
## 9 3.9 -0.00836 0.356
## 10 3 0.00866 0.318
## # … with 21 more rowspsi_est <- psi_search %>%
arrange(abs(estimate)) %>%
slice(1) %>%
select(-estimate, -p.value)We can get the confidence intervals by filtering out p-values with that are lower than .05 (since we’re looking for statistical independence) and take the minimum and maximum values of the estimate.
# get minimum and maximum values that have p >= .05 for confidence intervals
psi_conf_int <- psi_search %>%
filter(p.value >= .05) %>%
slice(c(1, n())) %>%
mutate(type = c("conf.low", "conf.high")) %>%
select(type, psi) %>%
spread(type, psi)
bind_cols(psi_est, psi_conf_int)## # A tibble: 1 x 3
## psi conf.high conf.low
## <dbl> <dbl> <dbl>
## 1 3.5 4.4 2.6The search ends up being linear (and, in fact, we can take a guess where the best h_psi will be based on the intercept of the regression line). Again, the closer we are to 0, the better.
psi_search %>%
ggplot(aes(x = psi, y = estimate)) +
geom_hline(yintercept = 0, col = "grey85", size = 1.3) +
geom_line(col = "#0072B2", size = 1.2) +
geom_point(shape = 21, col = "white", fill = "#0072B2", size = 2.5) +
theme_minimal(14)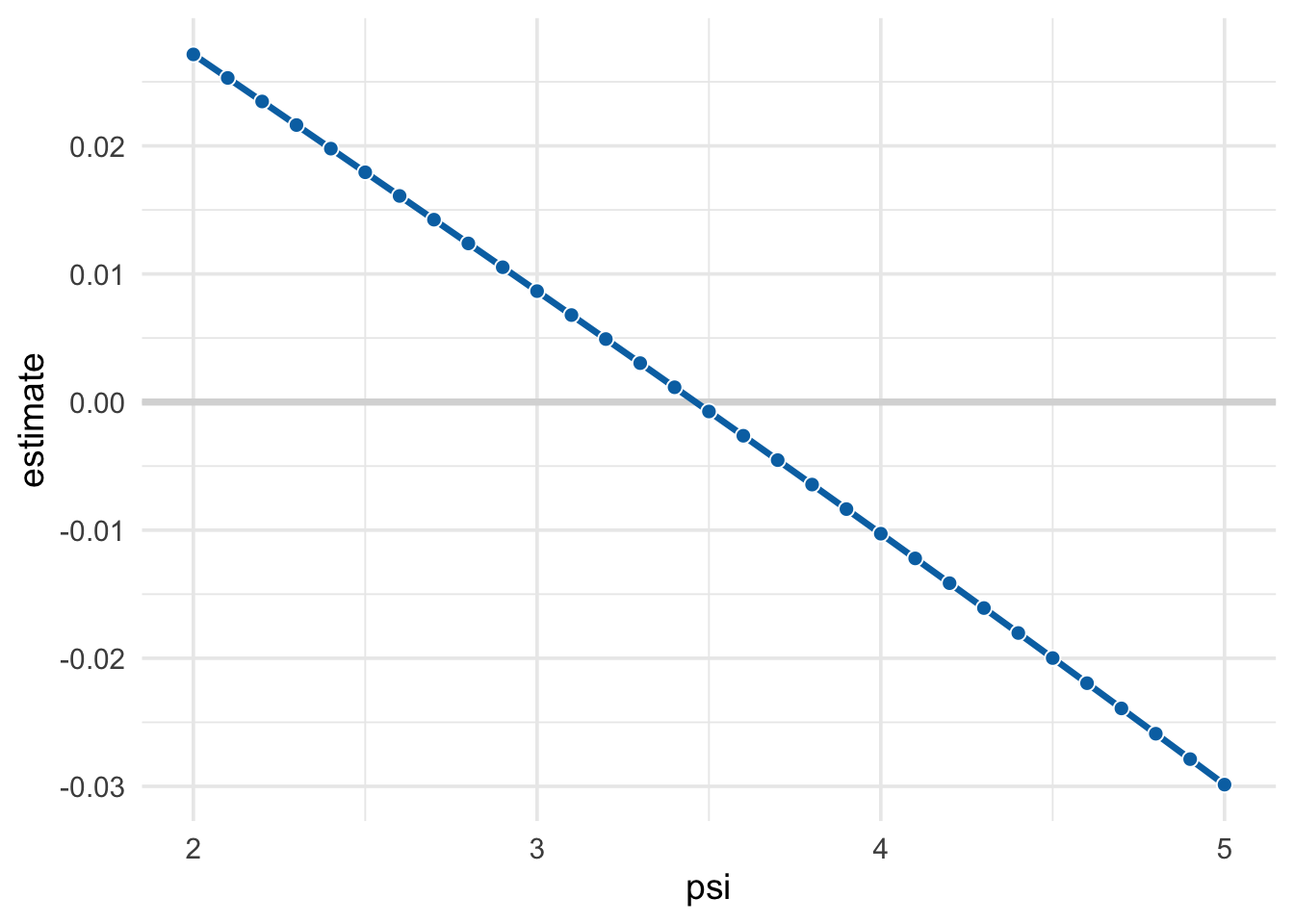
For some types of G-estimation models, we can use a closed-form estimator to predict psi using the censoring weights, outcome, treatment, and predicted treatment. First, we’ll calculate a model for qsmk (without h_psi) and then use these values to calculate psi using psi_formula().
psi_formula <- function(weights, outcome, treatment, treatment_pred) {
numerator <- weights * outcome * (treatment - treatment_pred)
denominator <- sum(weights * treatment * (treatment - treatment_pred), na.rm = TRUE)
sum(numerator / denominator, na.rm = TRUE)
}
estimate_psi <- function(.data) {
glm(
qsmk ~ sex + race + age + I(age^2) + education +
smokeintensity + I(smokeintensity^2) +
smokeyrs + I(smokeyrs^2) + exercise + active +
wt71 + I(wt71^2),
data = .data,
family = binomial(),
weights = cwts,
) %>%
augment(data = .data, type.predict = "response") %>%
summarize(
psi = psi_formula(
weights = cwts,
outcome = wt82_71,
treatment = qsmk,
treatment_pred = .fitted
)
)
}
nhefs_complete %>%
select(-.fitted:-.cooksd) %>%
filter(censored == 0) %>%
estimate_psi()## # A tibble: 1 x 1
## psi
## <dbl>
## 1 3.46As with other estimates, getting proper bootstraps involves writing a function to calculate the estimate using a re-sampled data set and then bootstrapping with the boot function.
bootstrap_psi <- function(data, indices) {
# calculate psi for the re-sampled data set
estimate_psi(data[indices, ]) %>% pull(psi)
}
bootstrapped_psis <- nhefs_complete %>%
select(-.fitted:-.cooksd) %>%
filter(censored == 0) %>%
boot(bootstrap_psi, R = 2000)
bootstrapped_psis %>%
tidy(conf.int = TRUE, conf.method = "bca")## # A tibble: 1 x 5
## statistic bias std.error conf.low conf.high
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 3.46 -0.00237 0.471 2.52 4.394.3 Program 14.3
Searching for more than one estimate, as in a model where we’re interested in the effect of both quitting smoking and baseline smoking intensity, is more difficult because it requires searching in two dimensions. For this example, we’ll use the closed-form estimator. Essentially, it requires two matrices with different combinations of products of qsmk, smokeintensity, wt82_71, and the model residuals. We’ll write a function to create and solve these matrices for us and give us two parameter estimates.
estimate_psi2 <- function(.data) {
glm(
qsmk ~ sex + race + age + I(age^2) + education +
smokeintensity + I(smokeintensity^2) +
smokeyrs + I(smokeyrs^2) + exercise + active +
wt71 + I(wt71^2),
data = .data,
family = binomial(),
weights = cwts,
) %>%
augment(data = .data, type.predict = "response") %>%
psi_formula2()
}
solve_matrix <- function(.data, .names = c("psi1", "psi2")) {
cells <- .data %>%
summarise(
a1 = sum(qsmk * diff),
a2 = sum(qsmk * smokeintensity * diff),
a3 = sum(qsmk * smokeintensity * diff),
a4 = sum(qsmk * smokeintensity * smokeintensity * diff),
b1 = sum(wt82_71 * diff),
b2 = sum(wt82_71 * smokeintensity * diff)
)
a <- cells %>%
select(a1:a4) %>%
unlist() %>%
matrix(2, 2)
b <- cells %>%
select(b1:b2) %>%
unlist() %>%
matrix(2, 1)
solve(a, b) %>%
t() %>%
as_tibble(.name_repair = "minimal") %>%
set_names(.names)
}
psi_formula2 <- function(.data) {
.data %>%
mutate(diff = (qsmk - .fitted) * cwts) %>%
drop_na(wt82_71) %>%
solve_matrix()
}
nhefs_complete %>%
select(-.fitted:-.cooksd) %>%
filter(censored == 0) %>%
estimate_psi2()## # A tibble: 1 x 2
## psi1 psi2
## <dbl> <dbl>
## 1 2.90 0.0287